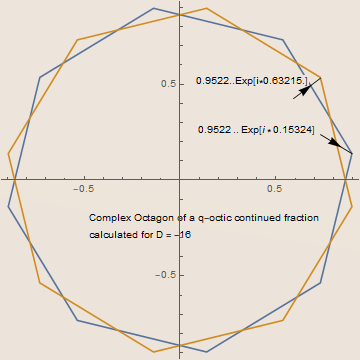
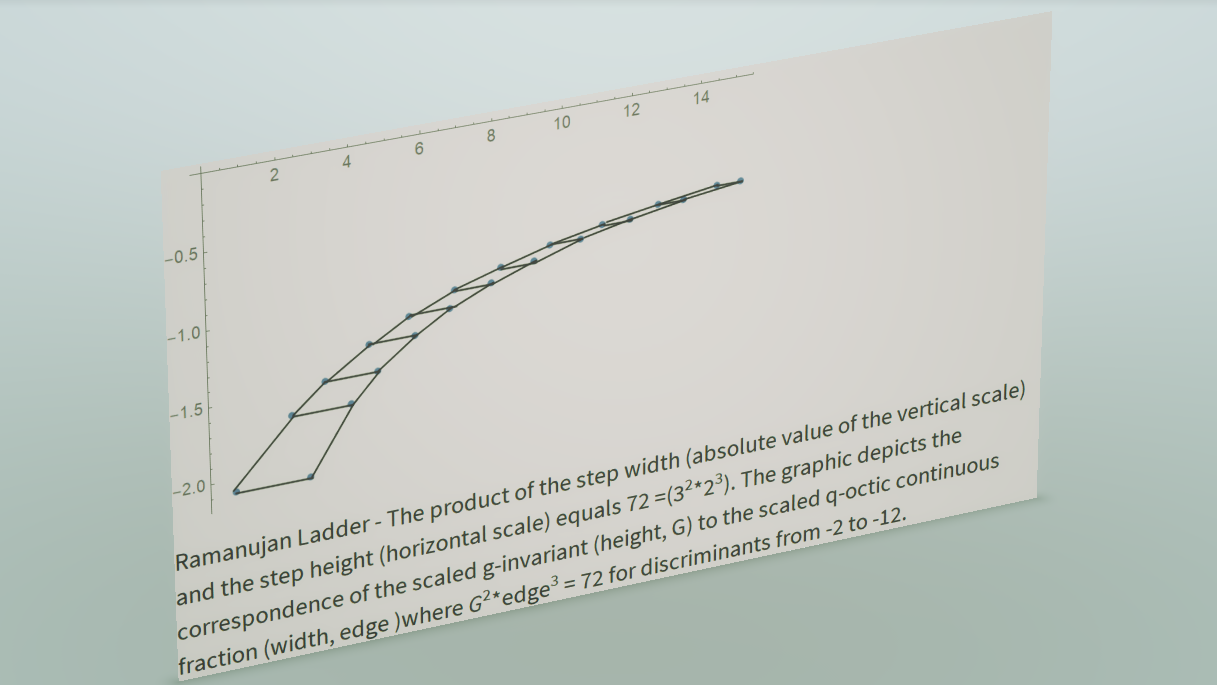
Welcome to the Perrin Chalkboard! I will be presenting in this blog a series of chalkboards which discuss interesting properties of the Perrin sequence and related integer sequences. This blog starts as a simple discussion of the Perrin sequence (the original mention by Lucas in 1876 and Perrin in 1899). It is found that an immense amount of research on the associated elliptic curves has occurred over the last 115 years. The Perrin sequence ties together much of the mathematics discussed today as algebraic number theory and modular functions. It is also integral to the discussion of Fermat’s Last Theorem conjectured in 1637 but proved by Wiles in 1994.
Theorems will be presented without proofs. I think the subject matter will appeal to those interested in the properties of integer sequences, elliptic equations, and graph theory. Many sequences from OEIS (On-line Encyclopedia of Integer Sequences) will be discussed, uncovering hidden or less obvious properties.
The primary subject matter in this blog covers the properties of integer sequences. However, it is not until Chapter 17 that I cover the subject matter of the short paper published by Perrin in 1899. This chapter then introduces the subject of integer partitions, followed by some geometric applications of the Perrin sequence and then turns to division algorithms derived from general properties of cubic equations and associated integer sequences.
I encourage any comments or suggestions to the chalkboard subjects.
Although the pdf files are freely provided, if you are interested or have questions regarding any chapter please feel free to contact me.
Richard Turk
March 2015
Updated July 2017
Click on the pdf to open the first chapter.. or continue scrolling to find the latest Chapter and pdf!